This short demonstration illustrates the use of the DCC model and its methods using the rmgarch package, and in particular an alternative method for 2-stage DCC estimation in the presence of the MVT distribution shape (nuisance) parameter. The theoretical background and representation of the model is detailed in the package’s vignette. The dataset and period used are purely for illustration purposes.
library(rmgarch) library(parallel) data(dji30retw) Dat = dji30retw[, 1:10, drop = FALSE] # define a DCCspec object: 2 stage estimation should usually always use # Normal for 1-stage (see below for xspec = ugarchspec(mean.model = list(armaOrder = c(1, 1)), variance.model = list(garchOrder = c(1,1), model = 'eGARCH'), distribution.model = 'norm') uspec = multispec(replicate(10, xspec)) spec1 = dccspec(uspec = uspec, dccOrder = c(1, 1), distribution = 'mvnorm') spec1a = dccspec(uspec = uspec, dccOrder = c(1, 1), model='aDCC', distribution = 'mvnorm') spec2 = dccspec(uspec = uspec, dccOrder = c(1, 1), distribution = 'mvlaplace') spec2a = dccspec(uspec = uspec, dccOrder = c(1, 1), model='aDCC', distribution = 'mvlaplace')
Since multiple DCC models are being estimated on the same dataset with the same first stage dynamics, we can estimate the first stage once and pass it to the dccfit routine (rather than re-estimating it every time dccfit is called):
cl = makePSOCKcluster(10) multf = multifit(uspec, Dat, cluster = cl)
Next, the second stage of the DCC model is estimated.
fit1 = dccfit(spec1, data = Dat, fit.control = list(eval.se = TRUE), fit = multf, cluster = cl) fit1a = dccfit(spec1a, data = Dat, fit.control = list(eval.se = TRUE), fit = multf, cluster = cl) fit2 = dccfit(spec2, data = Dat, fit.control = list(eval.se = TRUE), fit = multf, cluster = cl) fit2a = dccfit(spec2a, data = Dat, fit.control = list(eval.se = TRUE), fit = multf, cluster = cl)
To fit the DCC (MVT) model in practice, one either assumes a first stage QML, else must jointly estimate in 1 stage the common shape parameter. In the example that follows below, an alternative approach is used to approximate the common shape parameter.
# First Estimate a QML first stage model (multf already estimated). Then
# estimate the second stage shape parameter.
spec3 = dccspec(uspec = uspec, dccOrder = c(1, 1), distribution = 'mvt')
fit3 = dccfit(spec3, data = Dat, fit.control = list(eval.se = FALSE), fit = multf)
# obtain the multivariate shape parameter:
mvt.shape = rshape(fit3)
# Plug that into a fixed first stage model and iterate :
mvt.l = rep(0, 6)
mvt.s = rep(0, 6)
mvt.l[1] = likelihood(fit3)
mvt.s[1] = mvt.shape
for (i in 1:5) {
xspec = ugarchspec(mean.model = list(armaOrder = c(1, 1)), variance.model = list(garchOrder = c(1,1), model = 'eGARCH'), distribution.model = 'std', fixed.pars = list(shape = mvt.shape))
spec3 = dccspec(uspec = multispec(replicate(10, xspec)), dccOrder = c(1,1), distribution = 'mvt')
fit3 = dccfit(spec3, data = Dat, solver = 'solnp', fit.control = list(eval.se = FALSE))
mvt.shape = rshape(fit3)
mvt.l[i + 1] = likelihood(fit3)
mvt.s[i + 1] = mvt.shape
}
# Finally, once more, fixing the second stage shape parameter, and
# evaluating the standard errors
xspec = ugarchspec(mean.model = list(armaOrder = c(1, 1)), variance.model = list(garchOrder = c(1,1), model = 'eGARCH'), distribution.model = 'std', fixed.pars = list(shape = mvt.shape))
spec3 = dccspec(uspec = multispec(replicate(10, xspec)), dccOrder = c(1, 1), distribution = 'mvt', fixed.pars = list(shape = mvt.shape))
fit3 = dccfit(spec3, data = Dat, solver = 'solnp', fit.control = list(eval.se = TRUE), cluster = cl)
The plot in the change of the likelihood and shape shows that only a few iterations are necessary to converge to a stable value.
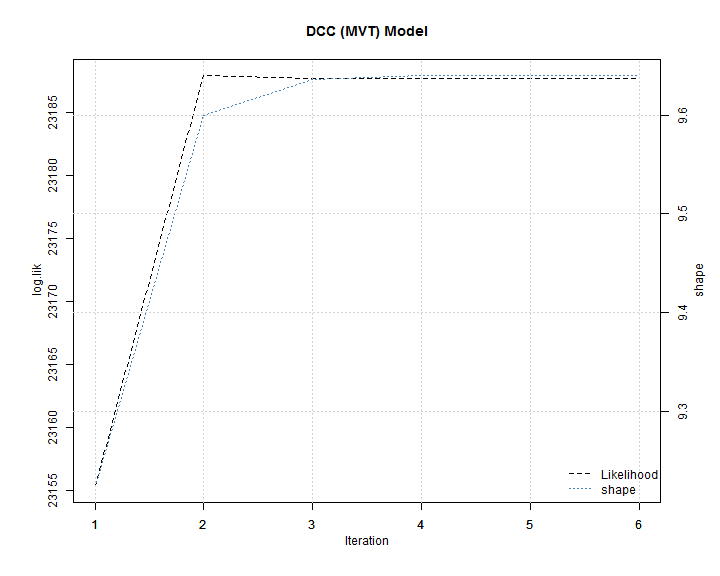
The value of the shape parameter implies an excess kurtosis of 1.06. The exercise is repeated for the asymmetric DCC (MVT) model.
xspec = ugarchspec(mean.model = list(armaOrder = c(1,1)), variance.model = list(garchOrder = c(1,1), model = "eGARCH"), distribution.model = "norm")
spec3a = dccspec(uspec = multispec( replicate(10, xspec) ), dccOrder = c(1,1), distribution = "mvt", model="aDCC")
fit3a = dccfit(spec3a, data = Dat, fit.control = list(eval.se=FALSE), fit = multf)
# obtain the multivariate shape parameter:
mvtx.shape = rshape(fit3a)
# Plug that into a fixed first stage model and iterate :
mvtx.l = rep(0, 6)
mvtx.s = rep(0, 6)
mvtx.l[1] = likelihood(fit3)
mvtx.s[1] = mvtx.shape
for(i in 1:5){
xspec = ugarchspec(mean.model = list(armaOrder = c(1,1)), variance.model = list(garchOrder = c(1,1), model = "eGARCH"), distribution.model = "std", fixed.pars = list(shape=mvtx.shape))
spec3a = dccspec(uspec = multispec( replicate(10, xspec) ), dccOrder = c(1,1), model="aDCC", distribution = "mvt")
fit3a = dccfit(spec3a, data = Dat, solver = "solnp", fit.control = list(eval.se=FALSE))
mvtx.shape = rshape(fit3a)
mvtx.l[i+1] = likelihood(fit3a)
mvtx.s[i+1] = mvtx.shape
}
# Finally, once more, fixing the second stage shaoe parameter, and evaluating the standard errors
xspec = ugarchspec(mean.model = list(armaOrder = c(1,1)), variance.model = list(garchOrder = c(1,1), model = "eGARCH"), distribution.model = "std", fixed.pars = list(shape=mvtx.shape))
spec3a = dccspec(uspec = multispec( replicate(10, xspec) ), dccOrder = c(1,1), model="aDCC", distribution = "mvt", fixed.pars=list(shape=mvtx.shape))
fit3a = dccfit(spec3a, data = Dat, solver = "solnp", fit.control = list(eval.se=TRUE), cluster = cl)
The table below displays the summary of the estimated models, where the stars next to the coefficients indicate the level of significance (*** 1%, ** 5%, * 10%). The asymmetry parameter is everywhere insignificant and, not surprisingly, the MVT distribution provides for the best overall fit (even when accounting for one extra parameter estimated).
## DCC-MVN aDCC-MVN DCC-MVL aDCC-MVL DCC-MVT aDCC-MVT ## a 0.00784*** 0.00639*** 0.00618*** 0.0055*** 0.00665*** 0.00623*** ## b 0.97119*** 0.96956*** 0.97624*** 0.97468*** 0.97841*** 0.97784*** ## g 0.00439 0.00237 0.00134 ## shape 9.63947*** 9.72587*** ## LogLik 22812 22814 22858 22859 23188 23188
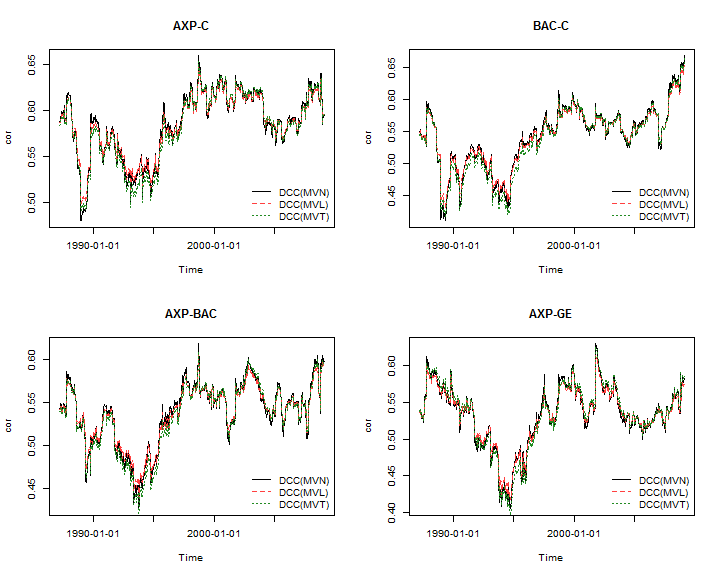
To complete the demonstration, the plots below illustrate some of the dynamic correlations from the different models:
…and remember to terminate the cluster object:
stopCluster(cl)