A frequently asked question relates to the minimum size of a dataset, required to obtain ‘good’ GARCH estimates. In this demonstration, the ugarchdistribution function is used to show how this question can be addressed within the rugarch package and the relevance of $\sqrt{N}$ consistency and how this relates to this question.
First define a GARCH specification
library(rugarch) library(parallel) cluster = makePSOCKcluster(10) spec = ugarchspec(mean.model = list(armaOrder = c(0, 0))) setfixed(spec)<-list(mu = 1e-04, omega = 3e-06, alpha1 = 0.05, beta1 = 0.92) sqrt(uncvariance(spec)) ## [1] 0.01
Now use this specification to simulate and estimate based on different data sizes.
mod = ugarchdistribution(spec, n.sim = 101, n.start = 1, m.sim = 100, recursive = TRUE, recursive.length = 3000, recursive.window = 250, cluster = cluster) # remember to terminate the cluster stopCluster(cluster)
The resulting object is of class uGARCHdistribution, with 3 slots:
slotNames(mod) ## [1] 'dist' 'truecoef' 'model'
The dist slot is a list of size equal to the number of estimated windows plus 1 (the last object in the list contains details of the estimation). Each list object contains the estimated parameters per window in addition to other calculated statistics for that window size. Next, we investigate the distribution of the parameters per window:
n = length(mod@dist) - 1
clr = topo.colors(n, alpha = 1)
mu = sapply(mod@dist, FUN = function(x) x$simcoef[, 1])
mu$details = NULL
omega = sapply(mod@dist, FUN = function(x) x$simcoef[, 2])
omega$details = NULL
alpha1 = sapply(mod@dist, FUN = function(x) x$simcoef[, 3])
alpha1$details = NULL
beta1 = sapply(mod@dist, FUN = function(x) x$simcoef[, 4])
beta1$details = NULL
par(mfrow = c(2, 2))
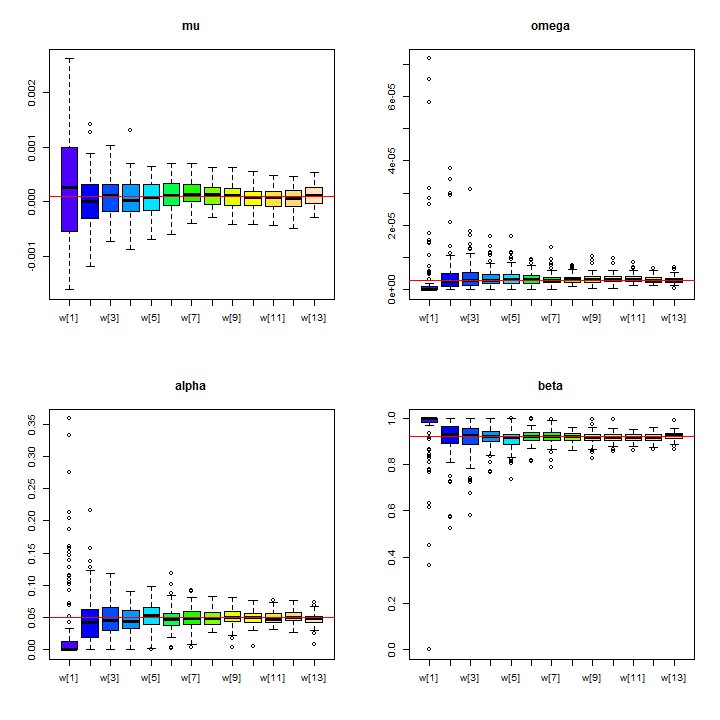
boxplot(na.omit(mu), names = paste('w[', 1:n, ']', sep = ''), col = clr)
abline(h = 1e-04, col = 2)
title('mu')
boxplot(na.omit(omega), names = paste('w[', 1:n, ']', sep = ''), col = clr)
abline(h = 3e-06, col = 2)
title('omega')
boxplot(na.omit(alpha1), names = paste('w[', 1:n, ']', sep = ''), col = clr)
abline(h = 0.05, col = 2)
title('alpha')
boxplot(na.omit(beta1), names = paste('w[', 1:n, ']', sep = ''), col = clr)
abline(h = 0.92, col = 2)
title('beta')
As expected, the standard deviation from the true parameter decreases as the window size increases, with the largest errors for the small window sizes. Another way to see this is via the root mean squared error (RMSE) plots:
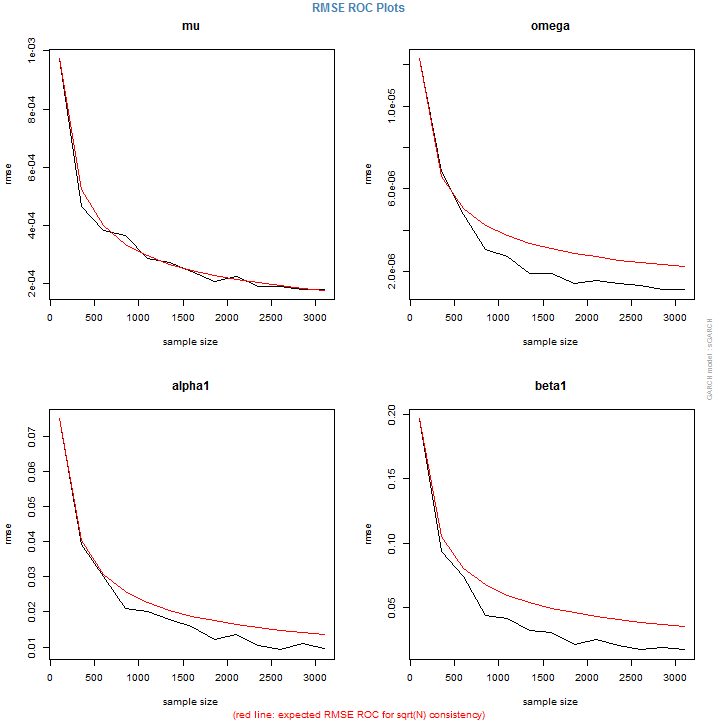
plot(mod, which = 4)
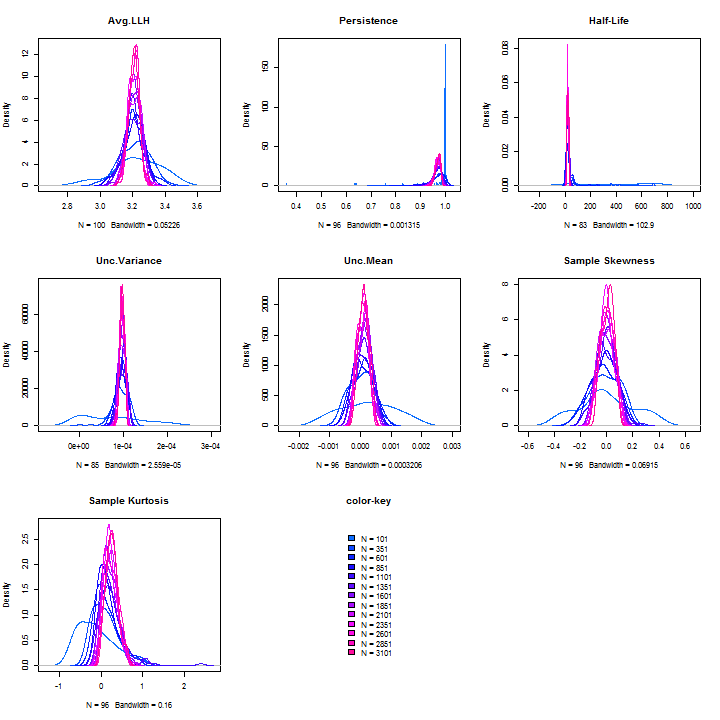
The plots show the RMSE of the fitted versus true coefficients per window size, and the red line the expected RMSE under the assumption of $\sqrt{N}$ consistency. As expected, more (data) leads to less (error). Finally, it it possible to investigate some additional plots showing the distribution of other measures of interest such as persistence, half-life etc:
plot(mod, which = 3)
The ugarchdistribution function makes it easy to investigate the importance of data size on the estimated parameters and provides an initial estimate of the cost of using too little data in GARCH estimation.
very good example!